“Experience with real-world data, however, soon convinces one that both stationarity and Gaussianity are fairy tales invented for the amusement of undergraduates.”
David Thomson

#Convolution - Cross-correlation - Auto-correlation

#Convolution - an operation on a Linear and Time Invariant system involving a given input signal and the impulse response.

#Cross-correlation - a measure of cross-similarity as a function of delay $\tau$

#Auto-correlation - a measure of self-similarity as a function of delay $\tau$

Recall: A convolution, $(h \ast x)(t)$, is a mathematical operator which manipulates two functions $x$ and $h$ and produces an output that represents the amount of overlap between $x$ and a reversed and translated version of $h$.

$$(x \ast h)(t) = \int_{-\infty}^{\infty} x(\tau)h(t - \tau) \, d\tau$$

Correlation

$$(f \star g)(\tau)\ = \int_{-\infty}^{\infty} f(t)\ g(t+\tau)\,dt$$

Thus, the only difference between cross-correlation and convolution is a time reversal on one of the inputs in convolution.

1. Cross-correlation , $(f \ast g)(t)$, produces a similarity measure that represents the amount of overlap between $f$ and a translated version of $g$.

(a) For finite duration waveform:

$$(f \star g)(\tau)\ = \int\_{T\_1}^{T_2} f(t)\ g(t+\tau)\,dt$$

if $f(t)$ exists in the interval $T_1 < t < T_2$

(b) For infinite duration waveforms:

$$(f \star g)(\tau)\ = \lim\_{T\to\infty} \dfrac{1}{T} \int_{\frac{-T}{2}}^{\frac{T}{2}} f(t)\ g(t+\tau)\,dt$$

2. Autocorrelation refers to the correlation of a signal with its own past and future values.

(a) For finite duration waveform:

$$(f \star f)(\tau)\ = \int\_{T\_1}^{T_2} f(t)\ f(t+\tau)\,dt$$

if $f(t)$ exists in the interval $T_1 < t < T_2$

(b) For infinite duration waveform:

$$(f \star f)(\tau)\ = \lim\_{T\to\infty} \dfrac{1}{T} \int_{\frac{-T}{2}}^{\frac{T}{2}} f(t)\ f(t+\tau)\,dt$$

(c) For a periodic waveform:

$$(f \star f)(\tau)\ = \dfrac{1}{T} \int\_{t\_0 }^{t_0 + T} f(t)\ f(t+\tau)\,dt$$

for an arbitrary $t_0$.

Example:

1. Find the autocorrelation function of the square pulse of amplitude a and duration T as shown below.

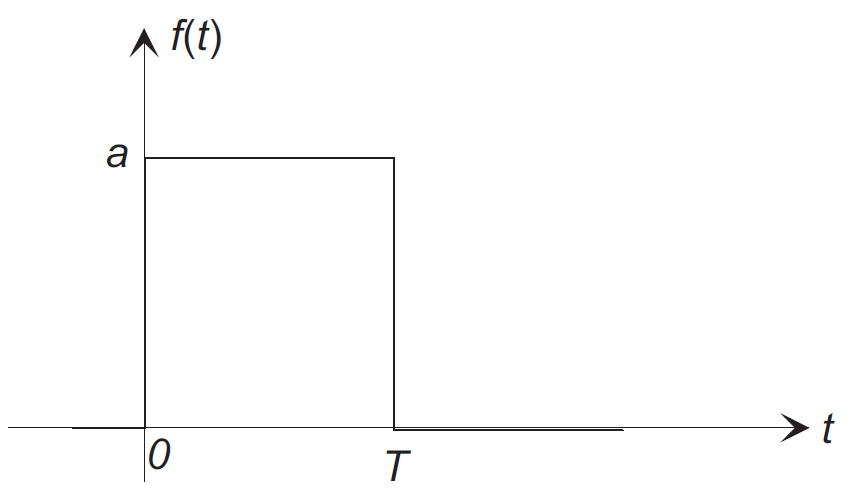
(a) Finite duration waveform:

$$(f \star f)(\tau)\ = \int_{0}^{T} f(t)\ f(t+\tau)\,dt$$

where $f(t)$ exists in the interval $0 \le t \le T$

The autocorrelation function is developed graphically below:

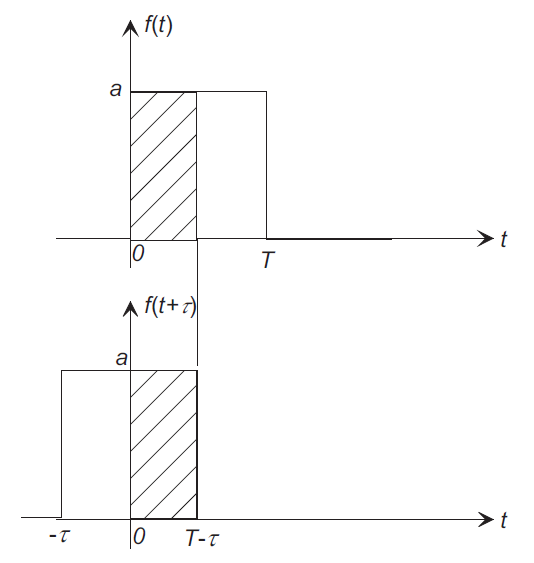
Case 1: Leading Edge Overlap

$$(f \star f)(\tau)\ = \int_{0}^{T-\left| \tau \right|} f(t)\ f(t+\tau)\,dt$$

where $f(t) = a$ exists in the interval $0 < t < T- \left

\tau \right

$

$$(f \star f)(\tau)\ = \int_{0}^{T- \left| \tau \right|} a a\,dt$$ $$(f \star f)(\tau)\ = a^2 \int_{0}^{T- \left| \tau \right|} \,dt$$ $$(f \star f)(\tau)\ = a^2 \left. t \right|_0^{T- \left| \tau \right|}$$ $$(f \star f)(\tau)\ = a^2 (T- \left| \tau \right|)$$

Case 2: Full Overlap

$$(f \star f)(\tau)\ = \int_{0}^{T} f(t)\ f(t+\tau)\,dt$$ $$(f \star f)(\tau)\ = \int_{0}^{T} a a\,dt$$ $$(f \star f)(\tau)\ = a^2 T$$

Case 3: Trailing Edge Overlap

$$(f \star f)(\tau)\ = \int_{\tau}^{T} f(t)\ f(t+\tau)\,dt$$

where $f(t) = a$ exists in the interval $T-\left

\tau \right

< t < T $

$$(f \star f)(\tau)\ = \int_{\tau}^{T} a a\,dt$$ $$(f \star f)(\tau)\ = a^2 \int_{\tau}^{T} \,dt$$ $$(f \star f)(\tau)\ = a^2 \left. t \right|_{\tau}^{T}$$ $$(f \star f)(\tau)\ = a^2 (T - \tau)$$

Thus, the autocorrelation is

$$(f \star f)(\tau) = \begin{cases} 0 & \mbox{if } -\infty < \tau < -T \\ a^2 (T - \left| \tau \right|) & \mbox{if } \, -T < \tau < T \\ 0 & \mbox{if } \, T < \tau < \infty \\ \end{cases}$$

or

$$(f \star f)(\tau) = \begin{cases} a^2 (T - \left| \tau \right|) & \mbox{if } \, -T < \tau < T \\ 0 & \mbox{otherwise } \\ \end{cases}$$

Reference: