Introductory Morphology

“Moment is a word which most often refers to an ambiguously short length of time, but also signifies in mathematics a quantitative measure of the shape of a set of points, and in physics relates to the perpendicular distance from a point to a line or a surface.”
Wikiquote

import numpy as np
from matplotlib import pyplot as plt, cm
%matplotlib inline
import skdemo
plt.rcParams['image.cmap'] = 'cubehelix'
plt.rcParams['image.interpolation'] = 'none'


image = np.array([[0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0]], dtype=np.uint8)
plt.imshow(image);

_config.yml

from skimage import morphology
sq = morphology.square(width=3)
dia = morphology.diamond(radius=1)
disk = morphology.disk(radius=2)
print(sq)
print('\n')
print(dia)
print('\n')
print(disk)

[[1 1 1]
 [1 1 1]
 [1 1 1]]


[[0 1 0]
 [1 1 1]
 [0 1 0]]


[[0 0 1 0 0]
 [0 1 1 1 0]
 [1 1 1 1 1]
 [0 1 1 1 0]
 [0 0 1 0 0]]



skdemo.imshow_all(image, morphology.erosion(image, sq), shape=(1, 2))

_config.yml

skdemo.imshow_all(image, morphology.dilation(image, sq))

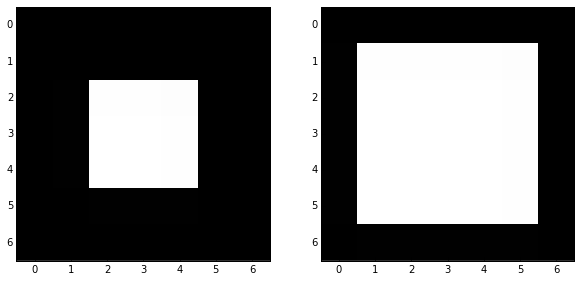
_config.yml

skdemo.imshow_all(image, morphology.erosion(image, dia))

_config.yml

skdemo.imshow_all(image, morphology.dilation(image, dia))

_config.yml

skdemo.imshow_all(image, morphology.erosion(image, disk))

_config.yml

skdemo.imshow_all(image, morphology.dilation(image, disk))

_config.yml

image = np.array([[0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0, 1, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0, 1, 0, 0],
                  [0, 0, 1, 1, 1, 0, 0, 1, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 1, 1, 1, 1, 1, 1, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0],
                  [0, 0, 0, 0, 0, 0, 0, 0, 0, 0]], np.uint8)
plt.imshow(image);

_config.yml

What happens when you run an erosion followed by a dilation of this image?

What about the reverse?

Try to imagine the operations in your head before trying them out below.

skdemo.imshow_all(image, morphology.opening(image, sq)) # erosion -> dilation

_config.yml

Opening result

skdemo.imshow_all(image, morphology.closing(image, sq)) # dilation -> erosion

_config.yml

Closing result

from skimage import data, color
hub = color.rgb2gray(data.hubble_deep_field()[350:450, 90:190])
plt.imshow(hub);

_config.yml

Remove the smaller objects to retrieve the large galaxy.

disk = morphology.disk(radius=2)
dst = morphology.erosion(hub, disk)
skdemo.imshow_with_histogram(dst)

(<matplotlib.axes._subplots.AxesSubplot at 0xadbe656c>,
 <matplotlib.axes._subplots.AxesSubplot at 0xadf49f2c>)

_config.yml

blob = dst > 0.5
plt.imshow(blob);

<matplotlib.image.AxesImage at 0xadf3fe2c>

_config.yml

from scipy import ndimage
label_im, nb_labels = ndimage.label(blob)

How many regions?

nb_labels

1

plt.imshow(label_im);

_config.yml

Size

sizes = ndimage.sum(blob, label_im, range(nb_labels+1))
print('sizes = ', sizes)

sizes =  [   0.  605.]

Center of Mass

print(ndimage.center_of_mass(blob))

(51.292079207920793, 33.214521452145213)

h,k = ndimage.center_of_mass(blob)
blob[h,k] = 0
plt.imshow(blob);

_config.yml

Written on April 5, 2015