Logistic Regression
Machine Learning Activity 3
%load_ext oct2py.ipython
Logistic Regression
from IPython.display import IFrame
IFrame('https://en.wikipedia.org/wiki/Logistic_regression', width='100%', height=540)
<iframe
width="100%"
height="540"
src="https://en.wikipedia.org/wiki/Logistic_regression"
frameborder="0"
allowfullscreen
></iframe>
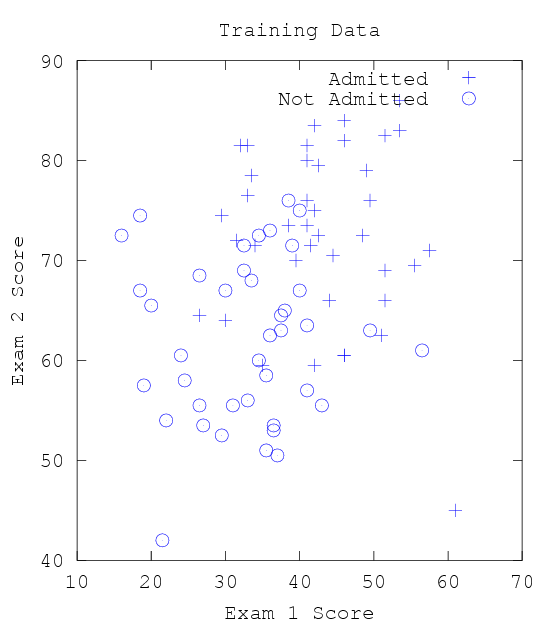
Load and Plot the data
%%octave
x = load('ml3x.dat');
y = load('ml3y.dat');
printf(" Test 1 Test 2 label\n")
format short g
[x y]
pass = find(y == 1);
fail = find(y == 0);
plot(x(pass, 1), x(pass,2), '+')
hold on
plot(x(fail, 1), x(fail, 2), 'o')
hold on
xlabel('Exam 1 Score')
ylabel('Exam 2 Score')
title('Training Data')
legend('Admitted', 'Not Admitted')
Test 1 Test 2 label
ans =
55.5 69.5 1
41 81.5 1
53.5 86 1
46 84 1
41 73.5 1
51.5 69 1
51 62.5 1
42 75 1
53.5 83 1
57.5 71 1
42.5 72.5 1
41 80 1
46 82 1
46 60.5 1
49.5 76 1
41 76 1
48.5 72.5 1
51.5 82.5 1
44.5 70.5 1
44 66 1
33 76.5 1
33.5 78.5 1
31.5 72 1
33 81.5 1
42 59.5 1
30 64 1
61 45 1
49 79 1
26.5 64.5 1
34 71.5 1
42 83.5 1
29.5 74.5 1
39.5 70 1
51.5 66 1
41.5 71.5 1
42.5 79.5 1
35 59.5 1
38.5 73.5 1
32 81.5 1
46 60.5 1
36.5 53 0
36.5 53.5 0
24 60.5 0
19 57.5 0
34.5 60 0
37.5 64.5 0
35.5 51 0
37 50.5 0
21.5 42 0
35.5 58.5 0
26.5 68.5 0
26.5 55.5 0
18.5 67 0
40 67 0
32.5 71.5 0
39 71.5 0
43 55.5 0
22 54 0
36 62.5 0
31 55.5 0
38.5 76 0
40 75 0
37.5 63 0
24.5 58 0
30 67 0
33 56 0
56.5 61 0
41 57 0
49.5 63 0
34.5 72.5 0
32.5 69 0
36 73 0
27 53.5 0
41 63.5 0
29.5 52.5 0
20 65.5 0
38 65 0
18.5 74.5 0
16 72.5 0
33.5 68 0
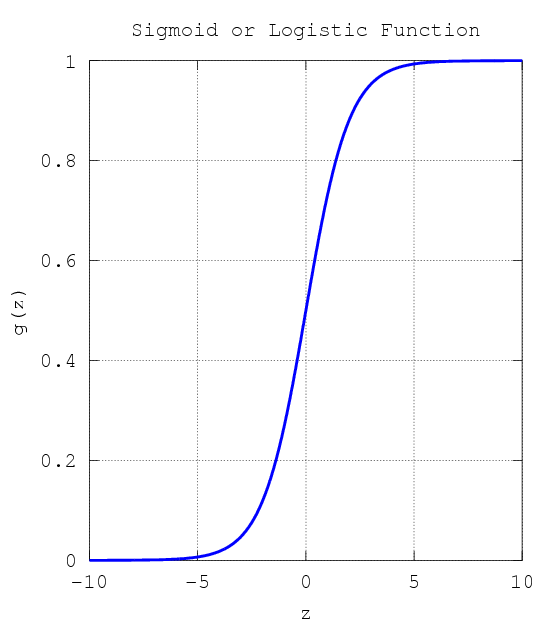
Hypothesis: Sigmoid or Logistic Function
%%octave
g = inline('1.0 ./ (1.0 + exp(-z))');
z = linspace(-10,10,1000);
plot(z,g(z),'linewidth',5);
xlabel('z');
ylabel('g(z)');
title('Sigmoid or Logistic Function');
grid on;
Newton’s Method and the Cost Function
%%octave
x = load('ml3x.dat');
y = load('ml3y.dat');
pass = find(y == 1);
fail = find(y == 0);
[m, n] = size(x); % m - no. of training data; n - no. of features
x = [ones(m, 1), x]; % Append ones for notation convenience
theta = zeros(n+1, 1); % n + 1 - no. of features + 1 (from the previous append)
g = inline('1.0 ./ (1.0 + exp(-z))'); % Sigmoid
MAX_ITERATION = 15;
J = zeros(MAX_ITERATION, 1);
for i = 1:MAX_ITERATION
z = x * theta; % Inner product, theta' * x
h = g(z); % Hypothesis
gradient = (1/m).*x' * (h-y);
H = (1/m).*x' * diag(h) * diag(1-h) * x;
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h)); % Cost Function
theta = theta - H\gradient;
end
plot(0:MAX_ITERATION-1, J, 'o-.', 'MarkerFaceColor', 'g', 'MarkerSize', 8)
xlabel('Iteration');
ylabel('J');
title('Cost Function');
grid on
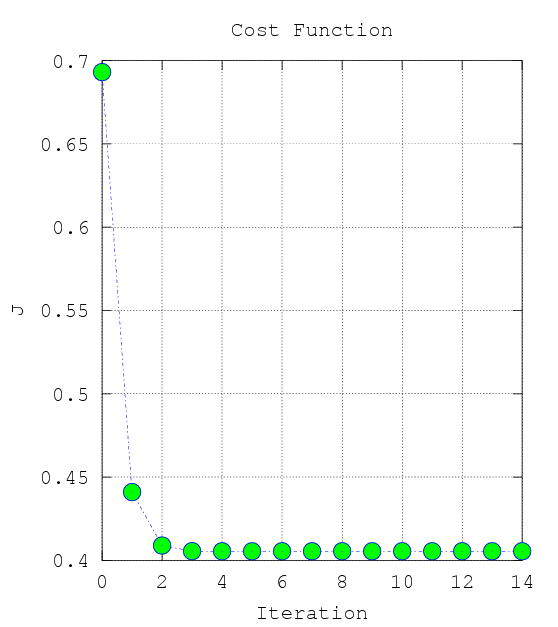
From this plot, you can infer that Newton’s Method has converged at around 4 - 7 iterations.
Cost Drop per Iteration
%%octave
x = load('ml3x.dat');
y = load('ml3y.dat');
pass = find(y == 1);
fail = find(y == 0);
[m, n] = size(x); % m - no. of training data; n - no. of features
x = [ones(m, 1), x]; % Append ones for notation convenience
theta = zeros(n+1, 1); % n + 1 - no. of features + 1 (from the previous append)
g = inline('1.0 ./ (1.0 + exp(-z))'); % Sigmoid
MAX_ITERATION = 6;
J = zeros(MAX_ITERATION, 1);
for i = 1:MAX_ITERATION
z = x * theta; % Inner product, theta' * x
h = g(z); % Hypothesis
gradient = (1/m).*x' * (h-y);
H = (1/m).*x' * diag(h) * diag(1-h) * x;
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h)); % Cost Function
theta = theta - H\gradient;
end
theta
cost_drop = J(2:MAX_ITERATION)-J(1:MAX_ITERATION-1)
theta =
-16.379
0.14834
0.15891
cost_drop =
-0.25221
-0.03205
-0.0033809
-6.3322e-05
-2.8988e-08
Thus, the convergence is the 5th iteration with a cost drop of about -2.8988e-08.
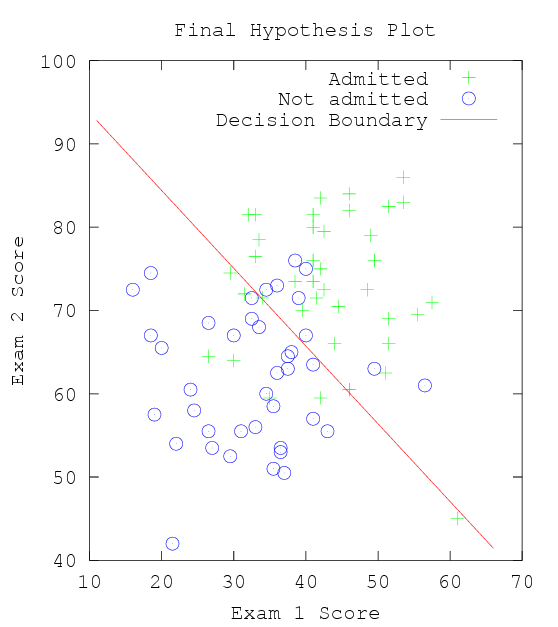
Final Hypothesis Plot
%%octave
x = load('ml3x.dat');
y = load('ml3y.dat');
pass = find(y == 1);
fail = find(y == 0);
plot(x(pass, 1), x(pass,2), 'g+')
hold on
plot(x(fail, 1), x(fail, 2), 'bo')
[m, n] = size(x); % m - no. of training data; n - no. of features
x = [ones(m, 1), x]; % Append ones for notation convenience
theta = zeros(n+1, 1); % n + 1 - no. of features + 1 (from the previous append)
g = inline('1.0 ./ (1.0 + exp(-z))'); % Sigmoid
MAX_ITERATION = 6;
J = zeros(MAX_ITERATION, 1);
for i = 1:MAX_ITERATION
z = x * theta; % Inner product, theta' * x
h = g(z); % Hypothesis
gradient = (1/m).*x' * (h-y);
H = (1/m).*x' * diag(h) * diag(1-h) * x;
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h)); % Cost Function
theta = theta - H\gradient;
end
x1_range = [min(x(:,2))-5, max(x(:,2))+5]; % +- 5 arbitrary allowance for the plot
x2_values = (-1./theta(3)).*(theta(2).*x1_range + theta(1)); % from theta' * x = 0
% theta_0 + theta_1*x_1 + theta_2*x_2 = 0
% Solving for x_2
% x_2 = (-1/theta_2).*(theta_0 + theta_1*x_1)
plot(x1_range, x2_values,'r-')
xlabel('Exam 1 Score')
ylabel('Exam 2 Score')
title('Final Hypothesis Plot')
legend('Admitted', 'Not admitted', 'Decision Boundary')
Prediction
What is the probability that a student with a score of 20 on Exam 1 and a score of 80 on Exam 2 will not be admitted?
%%octave
x = load('ml3x.dat');
y = load('ml3y.dat');
pass = find(y == 1);
fail = find(y == 0);
[m, n] = size(x); % m - no. of training data; n - no. of features
x = [ones(m, 1), x]; % Append ones for notation convenience
theta = zeros(n+1, 1); % n + 1 - no. of features + 1 (from the previous append)
g = inline('1.0 ./ (1.0 + exp(-z))'); % Sigmoid
MAX_ITERATION = 6;
J = zeros(MAX_ITERATION, 1);
for i = 1:MAX_ITERATION
z = x * theta; % Inner product, theta' * x
h = g(z); % Hypothesis
gradient = (1/m).*x' * (h-y);
H = (1/m).*x' * diag(h) * diag(1-h) * x;
J(i) =(1/m)*sum(-y.*log(h) - (1-y).*log(1-h)); % Cost Function
theta = theta - H\gradient;
end
probability = 1 - g([1, 20, 80]*theta)
probability = 0.66802
– based on Andrew Ng’s Machine Learning Course
– mkc
Written on September 23, 2015